convergent series test hard|convergence tests : mail order Strategy for Testing Series. We now have several ways of testing a series for convergence or divergence; the problem is to decide which test to use on which series. In this respect testing . webAssista vídeos pornô de Mostrando A Buceta de graça, aqui no Pornhub.com. Descubra a crescente coleção de vídeos e filmes Mais relevantes explícitos em alta qualidade. .
{plog:ftitle_list}
Significa apenas que você conectou-se a muitos dispositivos nos últimos dias. Isso também pode acontecer quando você compartilha seu login (o que é uma violação aos .
For problems 5 & 6 show that the series is divergent. Here is a set of practice problems to accompany the Convergence/Divergence of Series section of the Series & . When the test shows convergence it does not tell you what the series converges to, merely that it converges. Determine if \(~\displaystyle\sum_{n=1}^{\infty} \,\dfrac{n}{2^n}~\) .Look for low-hanging fruit: p-series, alternating series, geometric series. May need to do algebra or comparison to get to a form you can use. Use ratio test for exponential/factorial. Use root .Convergent series approaches a fixed value for its sum as the series approaches infinity. Learn how to identify convergent series here!
Strategy for Testing Series. We now have several ways of testing a series for convergence or divergence; the problem is to decide which test to use on which series. In this respect testing .
If a series is absolutely convergent, then it is convergent. (A series that converges but is not absolutely convergent is said to be conditionally convergent.) The .
if L> 1 L> 1 the series is divergent. if L = 1 L = 1 the series may be divergent, conditionally convergent, or absolutely convergent. In this section we give a general set of .
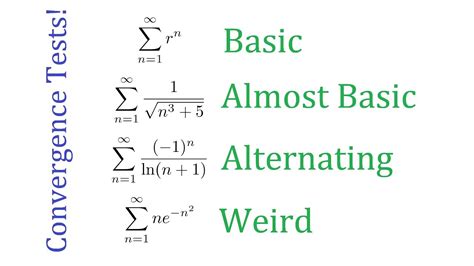
Testing for Convergence or Divergence of a Series. Many of the series you come across will fall into one of several basic types. Recognizing these types will help you decide which tests or .For each of the following series, determine which convergence test is the best to use and explain why. Then determine if the series converges or diverges. If the series is an alternating .
10.8 Alternating Series Test; 10.9 Absolute Convergence; 10.10 Ratio Test; 10.11 Root Test; 10.12 Strategy for Series; 10.13 Estimating the Value of a Series; 10.14 Power Series; 10.15 Power Series and Functions; 10.16 Taylor Series; . Just like with convergent series, adding/subtracting a finite number from a divergent series is not going to .We know exactly when these series converge and when they diverge. Here we show how to use the convergence or divergence of these series to prove convergence or divergence for other series, using a method called the comparison test. For example, consider the series \[\sum_{n=1}^∞\dfrac{1}{n^2+1}.\] This series looks similar to the convergent .
This technique is important because it is used to prove the divergence or convergence of many other series. This test, called the Integral Test, compares an infinite sum to an improper integral. It is important to note .
In order to use either test the terms of the infinite series must be positive. Proofs for both tests are also given. Paul's Online Notes. Notes Quick Nav Download. Go To; Notes; . As shown, we can write the series as a sum of two series and both of these series are convergent by the \(p\)-series test. Therefore, since each of these series are .For each of the following series, determine which convergence test is the best to use and explain why. Then determine if the series converges or diverges. If the series is an alternating series, determine whether it converges absolutely, converges conditionally, or diverges. How to do the series convergence tests for your Calculus 2 class. You will learn all types of convergence tests including direct comparison, telescoping seri.
Convergent test X∞ n=0 (−1)na n (a n > 0) converges if for alternating Series lim n→∞ a n = 0 and a n is decreasing Absolute Convergence for any series X∞ n=0 a n If X∞ n=0 |a n| converges, then X∞ n=0 a n converges, (definition of absolutely convergent series.) Conditional Convergence for any series X∞ n=0 a n if X∞ n=0 |a n .1.If we have an alternating series, then we always use the alternating series test. 2.If we see n! terms in the summation, then the ratio test will be our best choice. We can use the root test if nn or an appears and the ratio test is hard to compute. 3.If neither case 1 or 2 happen, then we should use the integral test or (limit) comparison test. The two conditions of the test are met and so by the Alternating Series Test the series is convergent. It should be pointed out that the rewrite we did in previous example only works because \(n\) is an integer and because of the presence of the \(\pi\). Without the \(\pi\) we couldn’t do this and if \(n\) wasn’t guaranteed to be an integer .
4b We use the Alternating Series Test, considering 2 n. n n a e = Note that ne2 án for most n with which we are con- cerned; therefore, we instead consider the rather simpler 1 n . n n ae e ==− This is a convergent geometric series. Since taking 1 2 nn n ee > as the summand also converges, this series is absolutely convergent.Convergence Test Calculator + Online Solver With Free Steps The Convergence Test Calculator is used to find out the convergence of a series. It works by applying a bunch of Tests on the series and finding out the result based on its reaction to those tests. Calculating the sum of a Diverging Series can be a very difficult task, and so is the case for any series to identify its .In mathematics, Dirichlet's test is a method of testing for the convergence of a series that is especially useful for proving conditional convergence. It is named after its author Peter Gustav Lejeune Dirichlet , and was published posthumously in the Journal de Mathématiques Pures et Appliquées in 1862.Deciding which convergence test to apply to a given series is often the hardest part of the unit on series convergence. In this video, I'm going to loosely w.
Here is a set of practice problems to accompany the Integral Test section of the Series & Sequences chapter of the notes for Paul Dawkins Calculus II course at Lamar University. Paul's Online Notes. Practice . 10.8 Alternating Series Test; 10.9 Absolute Convergence; 10.10 Ratio Test; 10.11 Root Test; 10.12 Strategy for Series; 10.13 .5.3.2 Use the integral test to determine the convergence of a series. 5.3.3 Estimate the value of a series by finding bounds on its remainder term. In the previous section, we determined the convergence or divergence of several .In mathematics, a series is the sum of the terms of an infinite sequence of numbers. More precisely, an infinite sequence (,,, .) defines a series S that is denoted = + + + = =. The n th partial sum S n is the sum of the first n terms of . Here is a convergence test for alternating series that exploits this structure, and that is really easy to apply. Theorem 3.3.14 Alternating Series Test. Let \(\big\{A_n\big\}_{n=1}^\infty\) be a sequence of real numbers that obeys . Alternating Series Test. works well when successive terms in the series alternate in sign;
What are Convergence Tests? Convergence tests are mathematical tools used to determine whether an infinite series converges or diverges. An infinite series is an expression of the form \sum_{n=1}^{\infty} a_n , where an represents the terms of the series. Convergence of a series implies that as more terms are added, the series approaches a finite value. Here is a set of practice problems to accompany the Absolute Convergence section of the Series & Sequences chapter of the notes for Paul Dawkins Calculus II course at Lamar University. Paul's Online Notes . 10.8 Alternating Series Test; 10.9 Absolute Convergence; 10.10 Ratio Test; 10.11 Root Test; 10.12 Strategy for Series; 10.13 Estimating .
We will also illustrate how the Ratio Test and Root Test can be used to determine the radius and interval of convergence for a power series. Paul's Online Notes. Notes Quick Nav Download. Go To; Notes; Practice Problems; . The inequality for divergence is just the interval for convergence that the test gives with the inequality switched and .
whether a series is convergent or divergent. If . a n has a form that is similar to one of the above, see whether you can use the comparison test: ∞. Geometric Series ∑ ∞ = − 1 1 n arn is. • convergent if r <1 • divergent if r ≥1 p-Series ∑ ∞ =1 1 n np is. • convergent if p >1 • divergent if p ≤1 Example: ∑ ∞ =1 . The Root Test can be used on any series, but unfortunately will not always yield a conclusive answer as to whether a series will converge absolutely or diverge. A proof of the Root Test is also given. . This is the last test for series convergence that we’re going to be looking at. As with the Ratio Test this test will also tell whether a . Recall that if a series is absolutely convergent then we will also know that it’s convergent and so we will often use it to simply determine the convergence of a series. Before proceeding with the test let’s do a quick reminder of factorials. This test will be particularly useful for series that contain factorials (and we will see some in . In order to use either test the terms of the infinite series must be positive. Proofs for both tests are also given. Alternating Series Test – In this section we will discuss using the Alternating Series Test to determine if an infinite series converges or diverges. The Alternating Series Test can be used only if the terms of the series .
They furnish simple examples of conditionally convergent series as well. There is a special test for alternating series that detects conditional convergence: Alternating series test: If \( a_n \) is a decreasing sequence of positive integers such that \( \lim\limits_{n\to\infty} a_n = 0 \), then \( \sum\limits_{n=1}^\infty (-1)^n a_n \) converges.Make a list of all the convergence tests you know. Students often feel overwhelmed because there are so many options, but in fact there are about 6 options, and on any given problem, 2-4 of those are obviously the wrong thing to do (the alternating series test only applies to alternating series, the integral test only applies to series with positive terms, etc).Review your knowledge of the various convergence tests with some challenging problems.
v20 volumetric karl fischer titrator vendor
web10 de jan. de 2024 · Hi, good day! I'm John Dev a Windows user like you and I'll be happy to assist you today. I know this has been difficult for you, Rest assured, I'm going to do my .
convergent series test hard|convergence tests